LU Matrix Decomposition in parallel with CUDA

The cublasStrsm() function allow us to solve linear systems in parallel but only when triangular matrix are involved.
For the general case, we need to perform a LU decomposition of the matrix beforehand.

For now,the Cublas library lack this feature  but almost all the Level 3 blass functions needed for the blocked LU decomposition are already available in Cublas.
The Blocked LU decomposition works like standard LU decomposition. But instead of applying the algorithm to digit, each step is performed onto block matrices.

Then lets start with the LU decomposition of a sample matrix before introducing the Blocked LU decomposition algorithm.

Standard LU decomposition :

From that we can compute easily  the first Row and the first column of L and U :

We can now rewrite (1)

if we regroup terms by block :

if we name :

Applying the block matrix product leads to :

Then, to compute 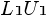, we can Apply  the same steps  to .

If we repeat the process until 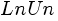is size 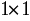. We get the LU decomposition of A

Finally :

I deliberately use a sample where we never need to divide by 0 (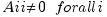). If it’s not the case a permutation matrix must be introduced to keep track of row pivoting.

Block LU decomposition :
Block LU decomposition is very similar to the algorithm we just described. The only difference is that we introduce the Block matrix at the beginning of the process.

We choose a sub matrix block size : 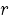and rewrite the matrix A of size 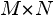as a block matrix:

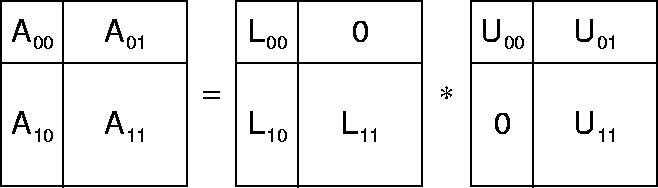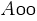Where is .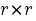

Like we did in the LU Decomposition section we can easily compute the first row and the first column of the L and U block matrices and apply the process iteratively to

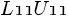As the usual rules of matrix multiplication hold with block matrices we can write

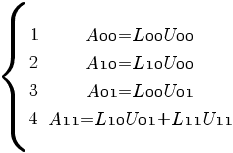From Eq(1) and (2) We can get 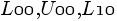applying LU decomposition (cf prev section) to the matrix  of size 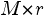composed by  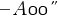and .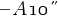

From Eq(3) we get

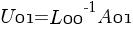Finally we rearrange Eq(4) as

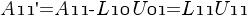From this equation we see that the problem of finding  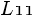 and 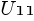reduces to finding the LU factorization of the 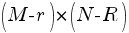matrix 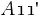. This can be done by applying the steps outlined above to 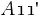instead of to A

For an in-place algorithm, A is overwritten by L and U – the 1s on the diagonal of L do not need to be stored explicitly. Similarly, when A is updated by Eq. (5) this may also be done in place. After k of these K steps, the first kr columns of L and the first kr rows of U have been evaluated, and matrix A has been updated to the form shown bellow.

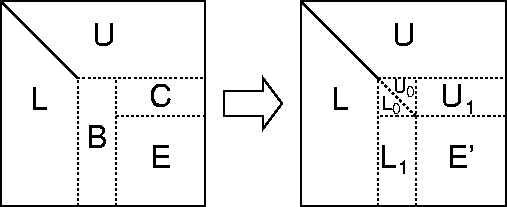Implementation :

As stressed in the previous section, we first need to implement the standard LU decomposition.

//***************************************************************************************
//void DecomposeLU( int M, int N, int lda , float* A,
//                    int* permute, float epsilon, InfoStat& stat)
//
// M         :     Num of rows of A
// N         :     Num of column of A
// A         :     Float Matrix of size M*N
//                on the output contains the result of the LU decomposition
//                The diagonal elements for L are not stored in A ( assuming they are all 1)
//lda        :    Leading dim of A lda < std::max(1,M)
//P          :      Permutation vector of size M
//epsilon    :     Epsilon (used to test for singularities)
//stat          :  return status
// **************************************************************************************
void DecomposeLU(int M, int N, int lda , float* A, int* P, float epsilon, InfoStat& stat)
{
     cublasStatus cuStat;
     //Preconditions
     if ( M<=0 || N<=0 || lda < std::max(1,M) )
     {
          stat._info = -1;
          if (M<=0)
              stat._str = "M<=0";
          if (N<=0)
              stat._str = "M<=0";
          if (lda < std::max(1,M))
              stat._str = "lda < std::max(1,M)";
          return;
     }
     int minDim = std::min( M, N );
     for (int k=0; k<minDim-1; k++)
     {
          int pivotRow = k-1+cublasIsamax(M-k,A+k + k*lda, 1); // row relative to the current submatrix
          int kp1 = k+1;
          P[k] = pivotRow;
          if (pivotRow!=k)
          {
               cublasSswap(N, A+pivotRow, lda, A+k, lda);
          }
          float valcheck;
          cublasGetVector(1,sizeof(float),A+k+ k*lda, 1, &valcheck, 1);
          if (fabs(valcheck) < epsilon)
          {
               stat._info =k+1;
               stat._str = " Matrix is Singular ";
               return;
          }
          if (kp1 < M)
         {
              cublasSscal(M-kp1, 1.0f/valcheck,A+kp1+ k*lda, 1);
         }
         if ( kp1 < minDim )
         {
              cublasSger (M-kp1, N-kp1, -1.0f,A+kp1+ k*lda, 1, A+k+ kp1*lda, lda,A+ kp1*lda+kp1, lda);
         }
     }
     CHECK_CUBLAS("decomposeLU pb");
}

As a further improvement, it would be nice to avoid the cublasGetVector() call. One solution would be to write this function as a kernel instead of using Cublas. Any other idea is welcome !

We can now use DecomposeLU() while performing the block decomposition :

//***************************************************************************************
//void DecomposeBlockedLU (	int M, int N,int lda,
//							float *A,
//							int* P, int blockSize,float epsilon, InfoStat &stat )
//
// M 			: 	Num of rows of A
// N 			: 	Num of column of A
// A 			: 	Float Matrix of size M*N
//					on the output contains the result of the LU decomposition
//					The diagonal elements for L are not stored in A ( assuming they are all 1)
//lda			:	Leading dim of A lda < std::max(1,M) //P 			:  	Permutation vector of size M //blockSize		:	Size of the submatrices //					if blockSize>=M || blockSize==1 unblocked decomposition is called
//epsilon		: 	Epsilon (used to test for singularities)
//stat 	 		:  return status
// **************************************************************************************
void DecomposeBlockedLU (	int M, int N,int lda,
							float *A,
							int* P, int blockSize,float epsilon, InfoStat &stat )
{

	cublasStatus cuStat;
	//Preconditions
	if (M < 0 || N < 0 || lda < std::max(1,M) )
	{
		stat._info = -1;
		if (M<=0)
			stat._str = "M<=0";
		if (N<=0)
			stat._str = "M<=0";
		if (lda < std::max(1,M))
			stat._str = "lda < std::max(1,M)"; 		return; 	} 	int minSize = std::min(M,N); 	if ( blockSize > minSize || blockSize == 1)
	{
		//straight LU decomposition
		DecomposeLU( M, N, lda, A, P, epsilon, stat);
	}
	else
	{
		//blocked decomposition
		for (int i =0; i< minSize ; i+=blockSize)
		{
			int realBlockSize  = std::min(minSize - i, blockSize);

			//decompose the current rectangular block
			DecomposeLU( M-i, realBlockSize, lda, A+i+i*lda, P+i, epsilon, stat);

			//adjust pivot infos
			//Todo : write a kernel for that
			for (int p = i; p< std::min( M, i+realBlockSize)-1; p++)
			{
					P[p] = P[p]+i;
					if (P[p] != p)
					{
						// Apply interchanges to columns 0:i.
						cublasSswap(i, A+p , lda, A+ P[p], lda);
						// Apply interchanges to columns i+blockSize:N.
						cublasSswap(N-i-realBlockSize, A+p+(i+realBlockSize)*lda , lda, A+ P[p]+(i+realBlockSize)*lda, lda);
					}

			}

			// Compute block row of U.
			cublasStrsm( 'l','l','n','u', realBlockSize, N-i-realBlockSize, 1.0f,
						 A +i +i*lda, lda, A +i + (i+realBlockSize)*lda, lda);
			CHECK_CUBLAS("decomposeBlockedLU cublasStrsm");

			if (i+realBlockSize < M)
			{
				 cublasSgemm('n','n',  M-i-realBlockSize, N-i-realBlockSize, realBlockSize,
							 -1.0f,
							 A+i+realBlockSize+i*lda,lda,
							 A+i+(realBlockSize+i)*lda,lda,
							 1.0f,
							 A+i+realBlockSize+(realBlockSize+i)*lda,lda );
				 CHECK_CUBLAS("decomposeBlockedLU cublasSgemm");
			}
		}
	}

}

Performances improvement :

For a random 10 000*10 000 matrix DecomposeBlockedLU run in about 3 second on my Quadro FX 4800 versus 98 second if we use DecomposeLU alone.

This code is used as a basis for Radial Basis Function interpolation computed on the GPU. I’m still eager to get better performances. I’m considering writing some part of it as a Cuda kernel. For any suggestion or if you know any alternative implementation available, thanks to drop me a mail or a comment.